Effort
A possibly new algorithm for LLM Inference
With Effort, you can smoothly adjust—in real time—the number of calculations performed during the inference of an LLM model.
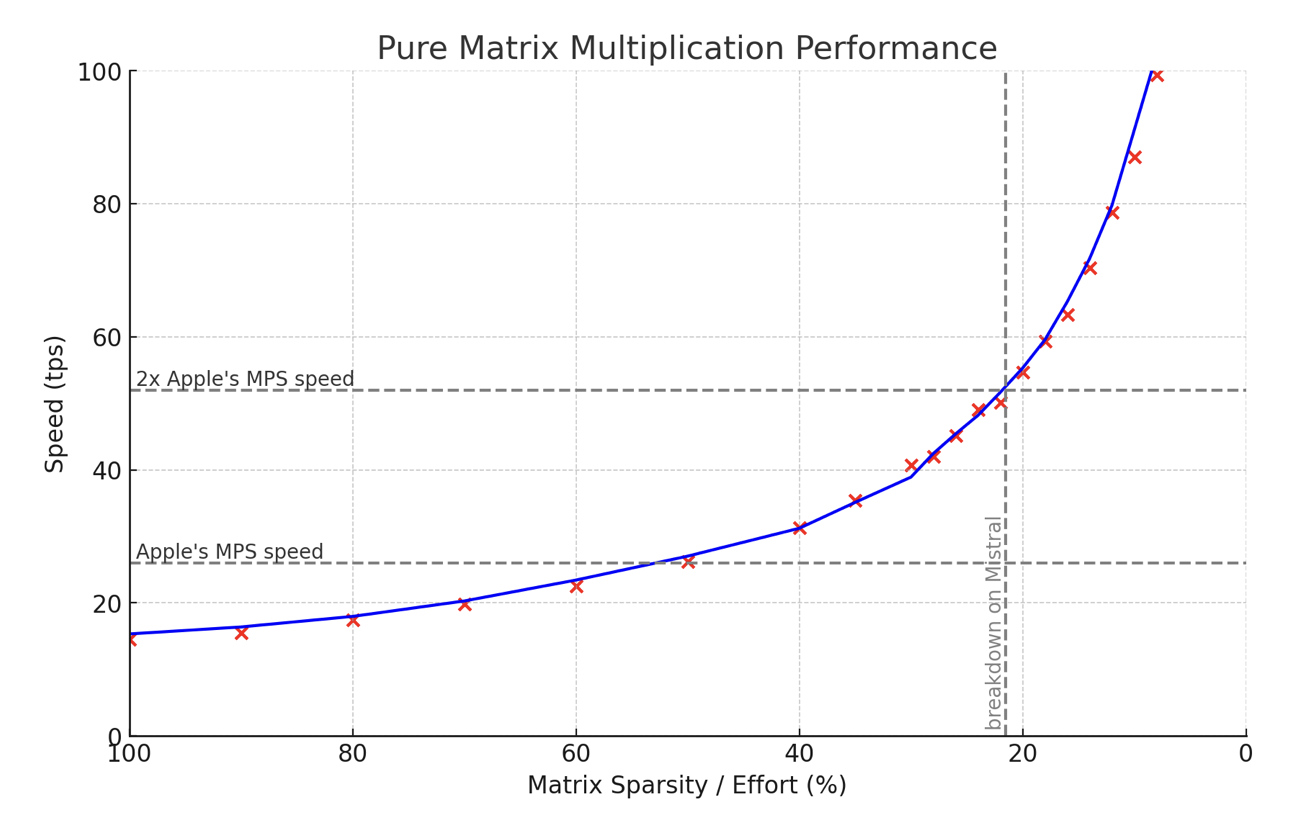
At 50% effort, it performs as fast as regular matrix multiplications on Apple Silicon chips; at 25% effort, it is twice as fast while still retaining most of the quality.
You also have the option to skip loading the least important weights.
It is currently implemented for Mistral, but it should work equally well for all other models without retraining—only conversion to a different format and some precomputation are necessary.
You can download the implementation here - from Github. It should run right after fetching the converted weights.
The implementation is done for FP16 only for now. The multiplications are fast, but the overall inference still requires improvement in some non-essential parts, such as softmax, attention summation etc. operations.
Mixtral and Q8 are in the works.
Oh, and there’s also the option to dynamically adjust how much of the model loads into memory. You can leave out the least important 10-20-30% of weights during loading. No conversion steps needed—it simply loads less data. It’s kind of like an ad-hoc distillation, if you will.
Let's see it in action now.
You can download and test it yourself from Github.
Returning to the topic of benchmarks...
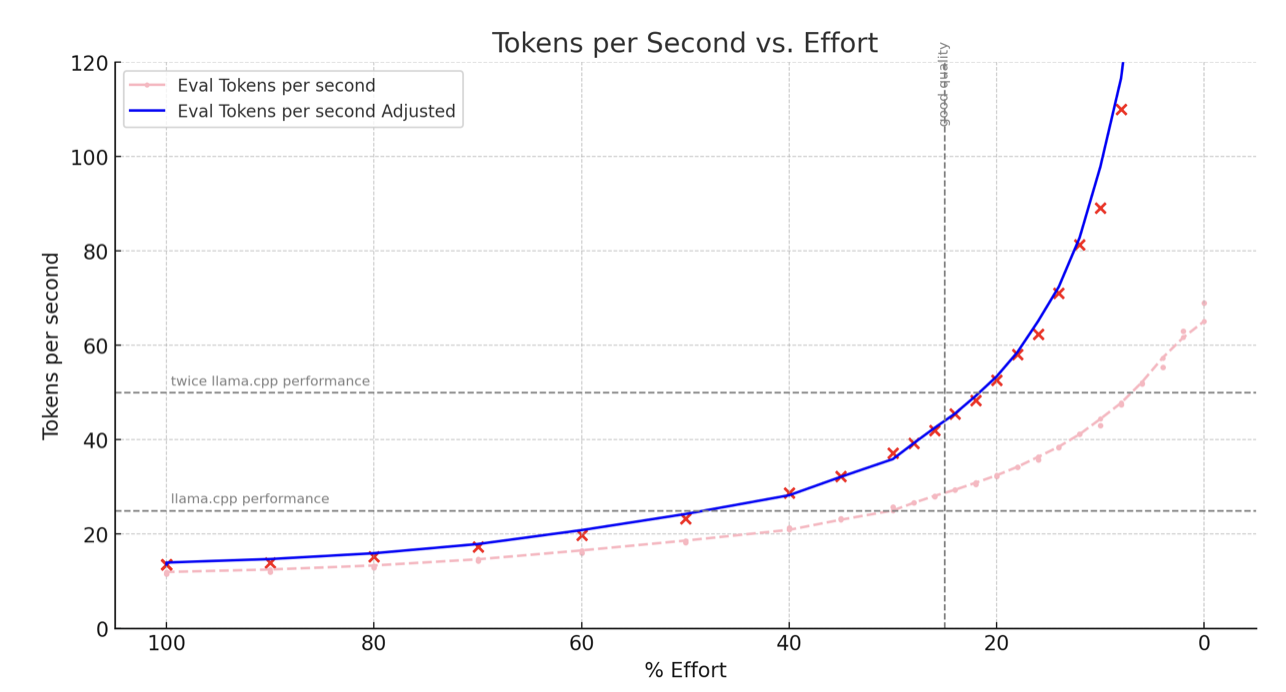 The pink line represents the actual speed, impacted by a suboptimal handling of overhead tasks (such as calculating norms and attention scores). Each token incurs an overhead of approximately 15ms, a problem not present in Llama.cpp, Ollama, or MLX. Help would be appreciated here from someone proficient in Metal/Swift.
The pink line represents the actual speed, impacted by a suboptimal handling of overhead tasks (such as calculating norms and attention scores). Each token incurs an overhead of approximately 15ms, a problem not present in Llama.cpp, Ollama, or MLX. Help would be appreciated here from someone proficient in Metal/Swift.
Let's now discuss quality, starting with the multiplication approximation itself.
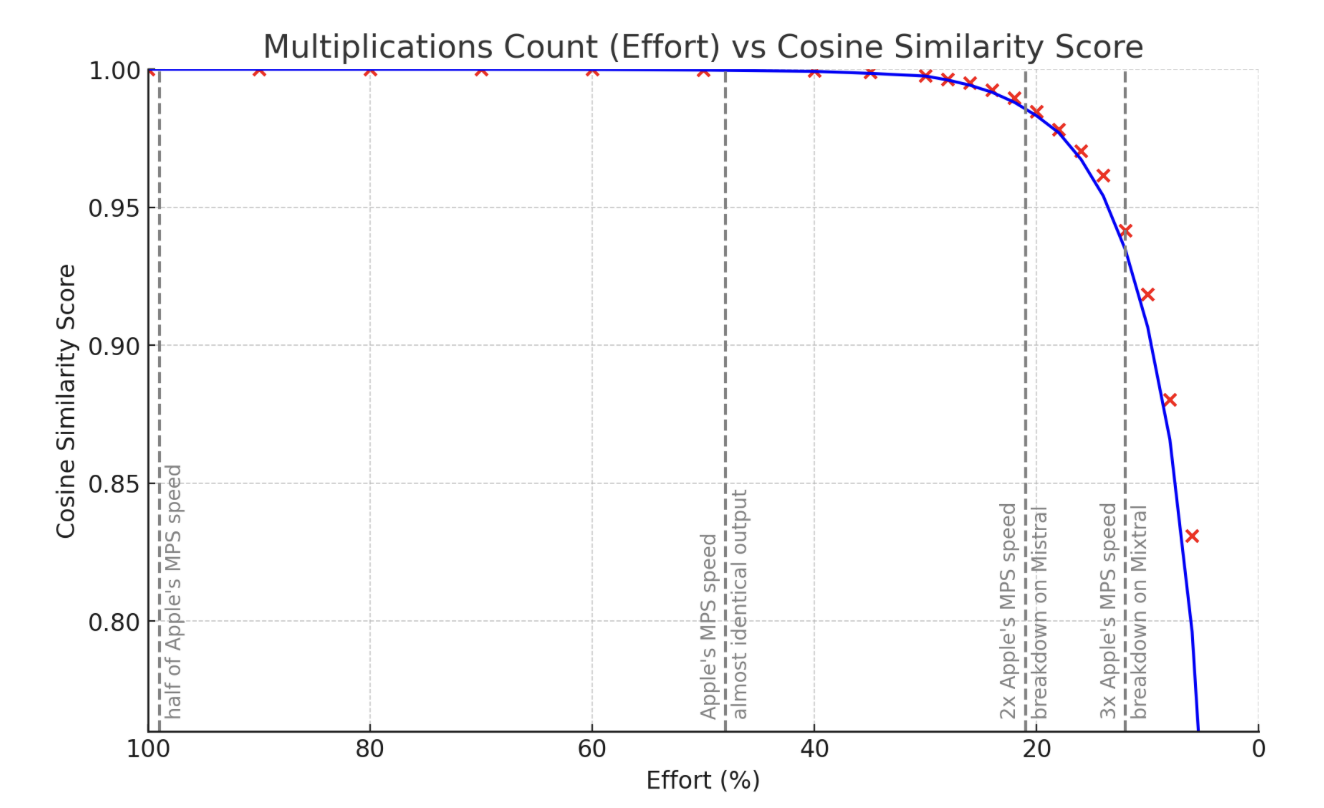 Quality is assessed by taking a sample input state vector and multiplying it by matrices such as wq or w1. Some matrices are easier to approximate using this method, while others are slightly more challenging. Overall, the output generally appears as shown here.
Quality is assessed by taking a sample input state vector and multiplying it by matrices such as wq or w1. Some matrices are easier to approximate using this method, while others are slightly more challenging. Overall, the output generally appears as shown here.
Turning our attention to the model itself.
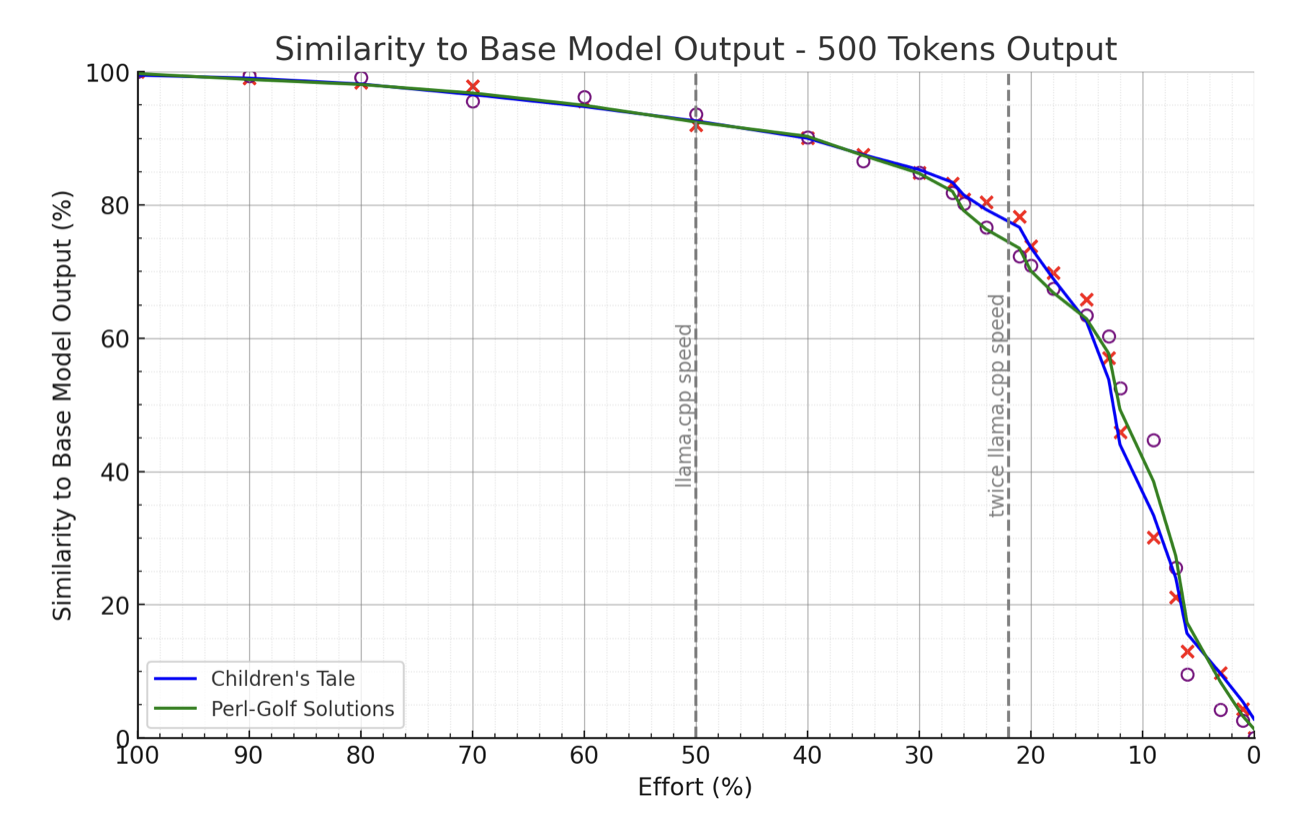 Performance is measured by first generating a 500-token text and then comparing the predictions of these tokens when the text is used as input.
Performance is measured by first generating a 500-token text and then comparing the predictions of these tokens when the text is used as input. Perplexity score would be nice here, see notes at the end why it's not yet done. KL Divergence tracking is in the works and should be released shortly.
And basic QA tests:
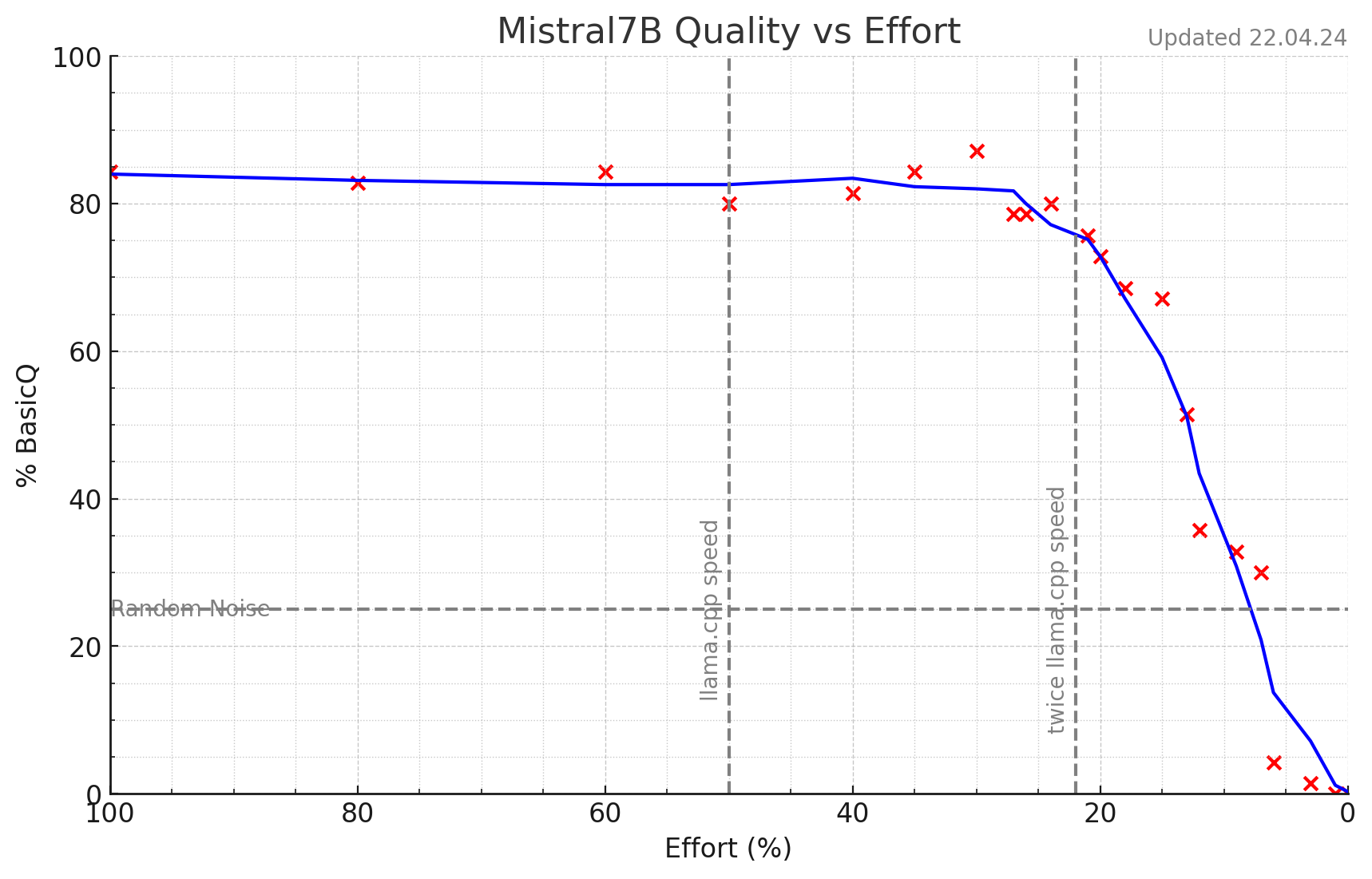 BasicQ consists of a series of a few tricky questions prepared by GPT-4. I hope this, along with the working demo, sufficiently demonstrates the potential. Before performing HumanEval and HellaSWAG, some fixes in the implementation are required—see details below.
BasicQ consists of a series of a few tricky questions prepared by GPT-4. I hope this, along with the working demo, sufficiently demonstrates the potential. Before performing HumanEval and HellaSWAG, some fixes in the implementation are required—see details below.
If you're still skeptical—as I would be—please visit the 'Help Needed!' section to understand what is required for improved testing.
The initial results (and undocumented experiments with Mixtral) seem to be robust enough to warrant publication. I hope though that the above is enough to convince you to play with the 0.0.1B version.
Deep dive into the algorithm.
- MoE, quantization and the others.
- Pesky details (or: Help Needed!)
And of course...
- - Citations, additional notes, and related resources
